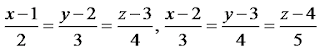B.Sc. (I YEAR) SEMESTER-II MATHEMATICS MODEL QUESTION PAPER ADIKAVI NANNAYA UNIVERSITY

MATHEMATICS MODEL PAPER

SECOND SEMESTER – SOLID GEOME TRY

COMMON FOR B.A & B.Sc

(w.e.f. 2016-17 admitted batch)

Time: 3 Hours                                                                              Maximum Marks: 75

SECTION-A

Answer any FIVE questions. Each question carries FIVE marks.     

                                                                                                               5 x 5 = 25 Marks

1. Find the equation of the plane through (4, 4, 0) and perpendicular to the planes            x + 2y +2z = 5 and 3x + 3y + 2z – 8 = 0.

 2. Find the image of a point (2, –1, 3)in the plane 3x – 2y + z =9.

3. Find the equation of the plane through the origin and containing the line                          x – 3y +2z+3 = 0=3x–y+2z–5.

4. Find the length of the perpendicular from the point (1, 2, 3) to the line through the point (6, 7, 7) whose d.r’s are 3, 2, –2.

5. Find the equation to the sphere through O = (0, 0, 0) and making intercepts a,    b, c on the axes.

 6. Find the polar line of

  w.r.t. the sphere 𝑥² + 𝑦² + 𝑧² = 16.

7. Find the equation to the cone which passes through the three coordinate axes    as well as the three lines

 and  

8. Find the enveloping cone of the sphere 𝑥² + 𝑦² + 𝑧² + 2𝑥 − 2𝑦 = 2 with its vertex             at (1, 1, 1).

SECTION-B

 Answer the all FIVE questions. Each carries TEN marks.         5 x 10 = 50 Marks

9(a). A variable plane is at a constant distance ‘p’ from the origin and meets the      coordinate axes in A,B,C. Show that the locus of the centroid of the            tetrahedron OABC is 𝑥⁻² + 𝑦⁻² + 𝑧⁻² = 16𝑝⁻²

Or

  (b). Find the bisecting plane of the acute angle between the planes 3x–2y+6z = 0,            –2x+y–2z–2 = 0.

 10(a). Find the S.D. between the lines  

       Find also  the equations and the points in which the S.D. meets the given lines.

Or

      (b) Prove that the lines

 are coplanar. Also find their point of intersection.

11(a) Find the equations of the spheres passing through the circle 𝑥² + 𝑦² = 4 ,                   z = 0 and is intersected by the plane x=+2y+2z = 0 in a circle of radius 3.

Or

     (b) Show that the spheres 𝑥² + 𝑦² + 𝑧² − 2𝑥 − 4𝑦 − 6𝑧 − 50 = 0 ,                                        𝑥² + 𝑦² + 𝑧² − 10𝑥 + 2𝑦 + 18𝑧 + 82 = 0 touch externally at the point  

 12(a) Find the limiting points of the coaxial system defined by spheres                                 𝑥² + 𝑦² + 𝑧² + 4𝑥 − 2𝑦 + 2𝑧 + 6 = 0 and 𝑥² + 𝑦² + 𝑧² + 2𝑥 − 4𝑦 − 2𝑧 + 6 = 0

Or

       (b) Find the equation of the lines of intersection of the plane 2x+y–z=0 and the                  cone 4𝑥² – 𝑦² + 3𝑧² = 0

13(a) Find the equation to the right circular cone whose vertex is P(2, –3, 5), axis   PQ which makes equal angles with the axis and which passes through        A(1, –2, 3).

Or

    (b) Find the equations of the tangent planes to the cone 9𝑥² − 4𝑦² + 16𝑧² = 0        which contains the line